Olimpiada de informatica
Faza nationala 1989

Proba teoretica

Utilizatori treapta I

1. In cate moduri poate fi ordonata multimea {1,2, ...,2n}, n apartine lui N , n>=1, astfel incat fiecare numar par sa aiba rang par? :
2. Sa se gaseasca p numere perfecte, unde p este dat. Precizam ca un numar natural este perfect daca este egal cu suma divizorilor lui, exceptand pe el insusi dar incluzand si pe 1.
(Exemplu: 28= 1+2+4+7+14)
3. Un poligon convex oarecare este dat in plan prin coordonatele varfurilor sale. Sa se gaseasca cea mai mare diagonala a sa.
4. Realizarea ciclurilor in limbajul BASIC HC-85.
5. Sa se scrie formalizat afirmatia: "Pentru orice numar intreg x, daca x nu este divizibil cu 3, atunci x² -1 este divizibil cu 3."

Nota: Precizarea pasilor algoritmului se face prin schema logica, sau in pseudocod sau prin descrierea matematica.

Utilizatori treapta II

1. Dati un algoritm pentru calculul catului si restului impartirii polinomului f apartine R[X] prin X - a. Cate adunari si inmultiri sunt necesare?

2. Fie f: N-->N data de f(x,y)=2^x*(2y+1)-1. Stiind ca f este bijectiva, sa se scrie un algoritm care pentru orice z apartine lui N determina x,y apartine N cu f(x,y)=z.

3. Sa se alcatuiasca un algoritm pentru calculul rezistentei echivalente a unui circuit format prin conectarea in serie si in paralel a unor rezistente de valori date. Circuitul este descris printr-un sir de caractere format din literele R, S, P astfel:

    - daca o componenta reprezinta o rezistenta, ea este descrisa prin R;
    - daca o componenta se obtine prin legarea in serie (respectiv in paralel) a doua alte componente, atunci se precizeaza mai intai cele doua componente, apoi litera S (respectiv P).

Exemplu: Circuitul


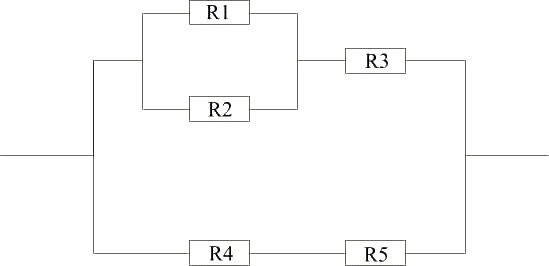
este descris prin RRPRSRRSP, valorile rezistentelor fiind apoi date in ordinea indicata de descrierea de mai sus a circuitului.
Precizare: Daca R' si R" sunt legate in serie (respectiv in paralel), rezistenta echivalenta este R'+R" (respectiv (R'*R")/(R'+R"))

4. Sa se prezinte modul de scriere a constantelor intregi si reale in limbajul BASIC.

5. Pentru orice doi vectori a,b de lungime n cu elemente in {0,1,2} se defineste vectorul c de lungime n astfel:

     /
    | ( a₁,...,a_i, 2,...,2 ) daca exista i apartine ( 1,...,n ) cu a_j=b_j, oricare ar fi j<i si a+b_i=1_i
    |
C=|
    |
    | (1,...,1)         in rest
     \
     Pentru a, b dati, sa se scrie algoritmul ce calculeaza vectorul c corespunzator.